How Transistors Become Calculating Machines

We learned in class that the basis of any electronic computational device found today is the transistor. For example, the most recent iPhone has 10 billion transistors in a chip that is only 122 square millimeters. But naturally, you might wonder how this computational "unit" can create such complicated functionality. I will try to explain that briefly in this post.

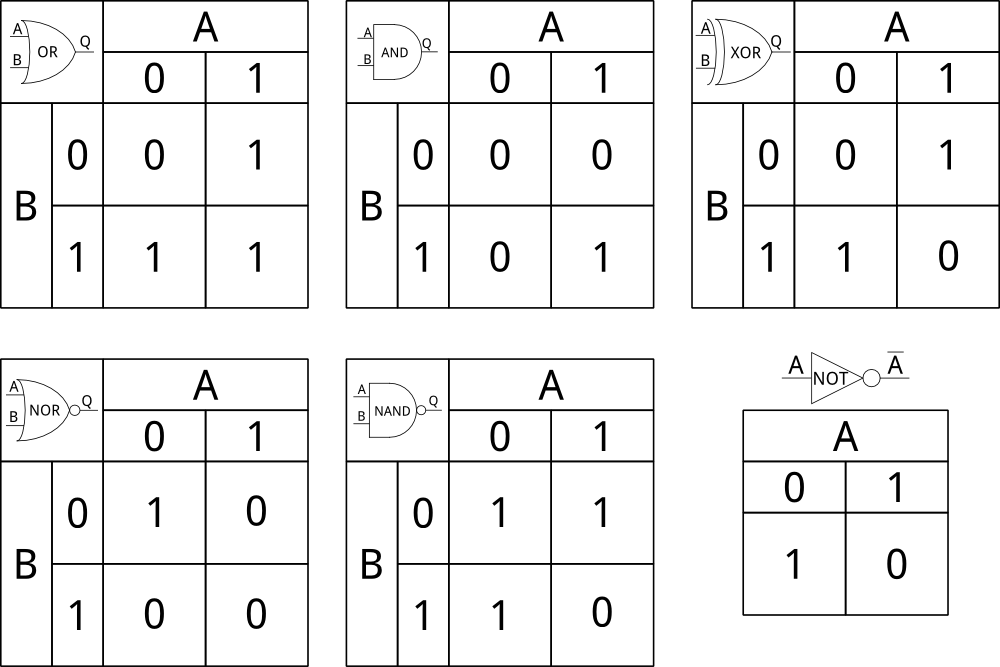
A transistor is most simply just a logic gate with two inputs and a single output. If both inputs are on then the output will be on. For any other combination, the output will be off. With this simple input-output rule (often called an AND gate because both inputs must be on) you can create several other logic gates such OR,  XOR,  NOT,  NAND, and NOR.  The different inputs and outputs are shown for all of these below.

The above logic gates are the most fundamental to boolean logic, and they can all be made using AND gates (a.k.a transistors), but I leave that as a challenge for someone in the comments. The question left is how do these more complex but still very simple logic gates create calculators. To demonstrate how I will show how simple adding works.

This simple adder would have three inputs (two single-digit numbers, A and B, in binary and a carry from a previous calculation) and two outputs (the value and what carries ever into the next sum). In a table format that would look like so.

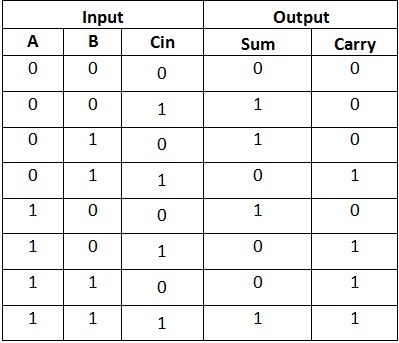
When the carry input is off, everything is simple. If you look at the sum column, you might notice that that is exactly the same as an XOR gate. Furthermore, the carry output column is exactly the same as an AND gate. When the carry input is turned on, the carry output is simply inverted. The sum column is a little more complicated when there is a carry bit. With the carry bit on, you want to XOR the input digits and then AND that with the carry input. In English, this means that if the "carry" is on and either A or B is on there will be a carry. This is put into an OR gate along with the AND result of the inputs. That way if both inputs are on and the carry is on the carry output will also be on. So a simple one-digit binary adder would look like this.

This might all seem very theoretical and difficult to understand, but if you take one step back and look at what we see here, it is very impressive. We have used a simple AND logic gate to create a complex machine that can add any two one-digit binary numbers. This machine can perform operations on numbers, and it is just made up of transistors. To add two 5-digit decimal numbers, you would need five of these, one for each digit. With millions of tiny adders like this one, you can create a machine that can surf the web, play Tetris, and help you write a blog.